Personal musings on new geometry and the state of journalistic integrity in the information age
by Adam Lore
Newly Discovered Forms
I really like polyhedra.
Okay, that is a bit of an understatement, I am completely obsessed with polyhedra! So when I heard that a new type of these shapes had supposedly been discovered I became very excited.
(Just really quickly, for anyone unfamiliar with the term, a polyhedron is a solid three dimensional geometric shape with straight edges and planar faces.)
As it turns out, though, the media coverage of this new finding at first left me totally confused about what was discovered. In the first articles I read, there were conflicting reports and major errors. It was unclear whether these were new at all, and there was a lack of clarity as to exactly what attributes these new shapes had.
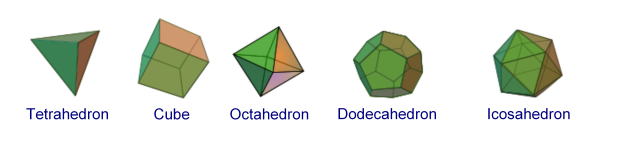
You see – my apologies to those of you who already know this stuff – people who study the attributes of polyhedra are usually interested in the ones that are highly symmetrical. One well known group is the group of Platonic Solids. A cube is one of these, because it is made of ‘regular’ polygons (squares), every polygon is the same, the polygons meet together at a vertex in the same way at the same angle, and none of the vertices is “caved in”. It becomes interesting to try to figure out which other shapes have all of these qualities, and to find that there are only 4 other shapes like this. (Now we have a problem. Both the 3rd group, the rhombic polyhedra, and the new, fourth group have more than one type of face, and many of the faces are not equiangular, thus not regular.)
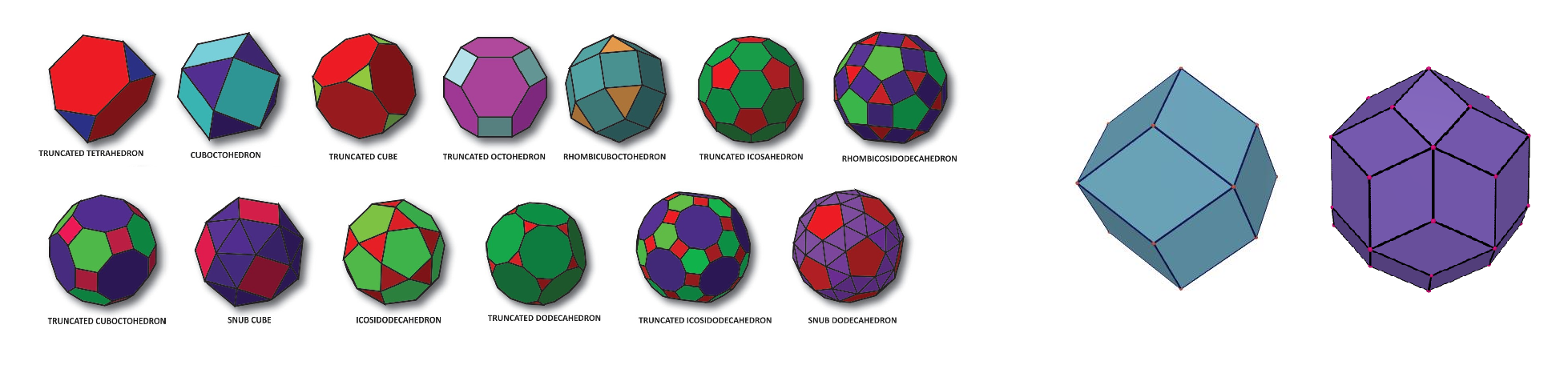
Then, if we allow the criteria to include polyhedra that are made out of 2 or more regular polygons instead of just one, we get 13 new ones, called the Archimedean Solids. (A rigid version of a soccer ball, also known as the truncated icosahedron, is a prime example of one of these.) By this new criterion we can also include prisms (which are just two of the same shape in the floor and ceiling, perhaps a pentagon, connected by squares along the rim) and anti-prisms (the same thing but with triangles instead of squares along the rim.) Then, there are some other ones, too, but the point is, there is a very specific limited amount of these things. (Problem: There are infinite numbers of prisms and antiprisms.)
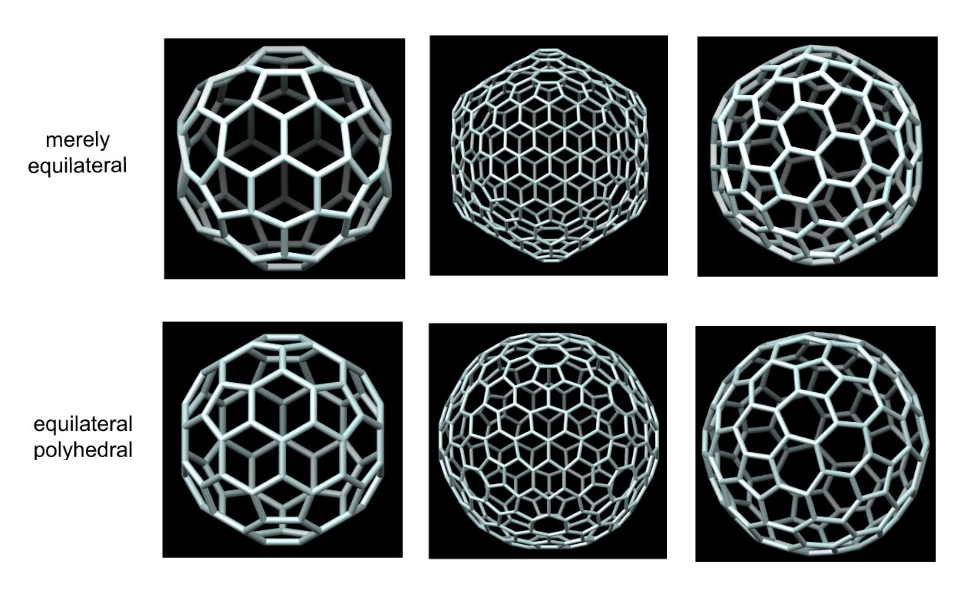
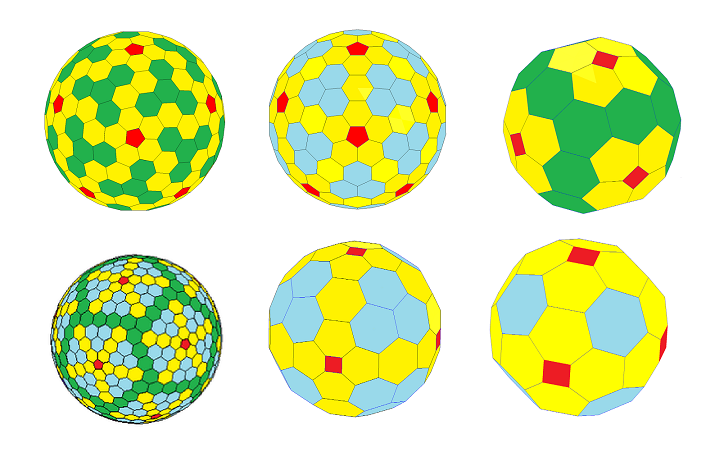
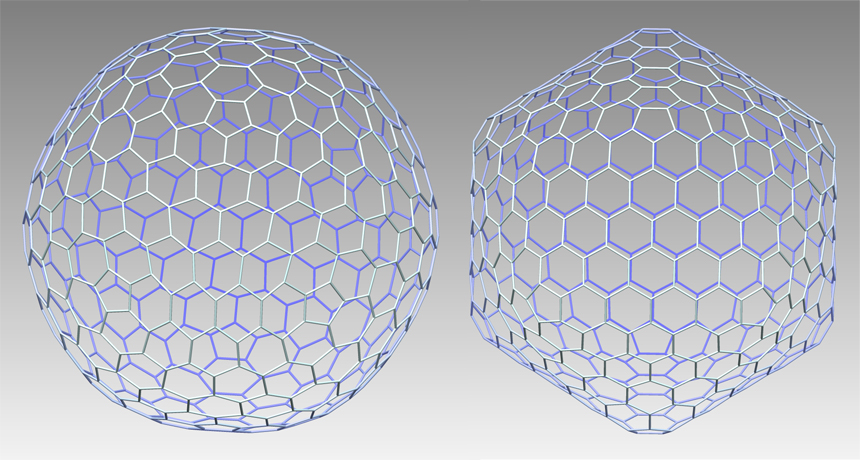
Just to be clear, the new forms are a modification of a previously known class of cages called Goldberg cages. (A cage can have nonplanar faces.) (Here I will be treating the modified forms as a group themselves). So, this newly discovered group of polyhedra by neuroscientists Stan Schein and James Gayed have the following attributes:
–They are convex, which means they do not have parts that are caved in,
–they do not have equal angles but they do have equilateral edges (meaning each edge is the same length), and
–all of their faces are “planar”, which is very important, meaning that the faces lie flat and do not bulge in or out.
At first I thought that mathematician and polyhedron model builder George W. Hart had already worked out the math for these same shapes, but he confirmed via e-mail that the models he had made “have planar faces but generally are not equilateral. So, their result is new because of the equilateral property and (in my quick reading) appears to be correct.” (Thanks, George!) In a recent Science News article on the subject mathematician Branko Grünbaum makes the same confirmation, “It is correct, and the result is new.”
The Schein-Gayed Innovation
So, basically what Schein and Gayed did was they took a previously known group of ‘Goldberg cages’ with icosahedral, octahedral and tetrahedral symmetry, described back in 1937 by mathematician Michael Goldberg, and modified them. The original Goldberg cages bulged out and did not have edges of equal length. Later, George Hart made modified versions that did not bulge out before, but those did not have equal edges. Schein and Gayed worked out the necessary math and modified the Goldberg cages to be both planar and equilateral, thus convex equilateral Golderg polyhedra with polyhedral symmetry! (An object with ‘polyhedral symmetry’ has icosahedral, octahedral or tetrahedral symmetry.) Their discovery adds one new class to what were previously only 3 known classes of convex equilateral polyhedra with polyhedral symmetry. So you see, what they did was actually quite innovative and – in my view – a pretty important discovery in this particular field of study.
Now, it took me a while to sort all of this out. The articles that showed up on Google news had conflicting reports and major errors. The best article* out there did not show up in the search results. A particularly atrocious little article on Gizmodo.com (called “These Brand New Shapes Are a Class of Their Own” by PJ Smith) mistakenly reports that the new shapes have equal sides and equal angles, “a combo that’s actually never been seen before.” This is completely false, in more ways than one. In fact, I could be wrong, but as far as I can tell, every single sentence in the first two paragraphs of the Gizmodo articles is incorrect!
(the best article: science news: https://www.sciencenews.org/article/goldberg-variations-new-shapes-molecular-cages)
http://gizmodo.com/these-brand-new-shapes-are-a-class-of-their-own-1523136222
Gizmodo Falsehoods
Gizmodo: “The criteria for being your own type of three dimensional solid is all about whether your edges are equal lengths, and whether your faces are regular polygons.”
This is false.
Gizmodo: “Discovered by UCLA neuroscientist Stan Schein and UCLA neuroscientist James Gayed, Goldberg polyhedra (pictured left) do have sides that are all the same length, but its polygonal faces have equal angles.”
Doubly false- Schein-Gayed versions of the Goldberg Polyhedra were on the right (not the left) and the faces do not have equal angles.
Gizmodo: “And surprisingly enough, that’s a combo that’s actually never been seen before.”
False, combinations of equal edges and equal angles have been seen before, as well as combinations of just equal edges.
Gizmodo: “The Goldberg polyhedra’s properties, specifically their equal angles, give them a rounded, spherical appearance.”
False, they don’t have equal angles so their spherical appearance could not possibly arise from having equal angles.
I am not going to go through the whole thing, but I think you get the point. How is it that this is what passes for journalism today? This guy just copied an article from another website, an article that was almost as far off from the truth, went further and misunderstood every detail of the first article, took no effort to check his facts, obviously did not consider looking at the original research paper, and turned in and published pure garbage. What is even the point of writing about something if literally every single sentence is wrong? Why is this considered acceptable? Why do we not have higher standards than this?
“All of these classes of polyhedra are wonderful. Why compare?”
Another frustrating aspect of this is the outright dismissal by some sources of Schein and Gayed’s findings. One article by the Daily Mail is entitled: “Scientists discover a new SHAPE for the first time in 400 years (but it just looks like a football)”, as if there have been no new shapes discovered since the 1600’s, completely ignoring the works of Coxeter, Penrose, John H. Conway, Gosset, Schlaffli, J. C. P. Miller, Michael Longuet-Higgins, Norman Johnson, Steve Waterman, or Nikolai Lobachevsky, to name just a few. Reducing the findings to “but it looks just like a football” is all too typical.
Correspondingly, the Comment sections are filled with smart aleck remarks of this nature:
Weeding through this kind of misinformation and utter garbage is the burden of the information edge.
Beautiful Objects – an Interview with STAN SCHEIN
“We never gave any thought to applications.
We are basic scientists interested in beautiful objects”
But so on the bright side, which really is the side we should be focusing on, Schein and Gayed’s original paper on the topic was easy to find, an excellent read, and along with it was Stan Schein’s e-mail address. I sent him a quick e-mail, and he promptly responded, recommending the much better article in Science News, which I also highly recommend to anyone interested in the topic!. Stan was very polite and accommodating, responding back and forth several times, asking what my own field of study was, and clarifying my misunderstandings from poorly written articles. He even allowed me to conduct a little mini-interview with him!
James Gayed and you seem to have discovered not just a new sub-group of polyhedra, but an entirely new approach to finding new forms that seems to have been overlooked by mathematicians until now. Do you anticipate this leading to more discoveries soon by other researchers using the same method and applying it to different groups of shapes?
Schein: We use the Goldberg construction, dating to 1937, to generate the cages. Not new. We do have a new approach to transforming these to polyhedra. We ourselves hope to discover more new cages and polyhedra. How soon others do it, we cannot say.
How do you feel the public and the media have responded to your new findings? Do you feel your work has been under appreciated, over exaggerated, misunderstood? Any notable clarifications you would make to articles that have been published?
Schein: We are surprised by the level of interest. We are impressed by some of the coverage, particularly the article in Science News, the PNAS blog, and a piece in Der Spiegel (in German).
Are you aware of any interesting properties of the duals of this sub-class of Goldberg polyhedra? (For example, the dual of a cube being an octahedron, replacing the faces with vertices.) It would seem that some level of symmetry would be lost, but traded for another.
We do not see much that is interesting in the duals of these Goldberg polyhedra. But, please note that the dual of a cage or polyhedron has the same symmetry as the original.
Do you feel that there is something particularly more appealing or useful, more important, about the particular combination of a polyhedron being convex, planar, and having equilateral sides and polyhedral symmetry? Do you think that other classes of polyhedra with high symmetry in other ways but that lack one of these are less important?
We began with an interest in self-assembly. The ‘parts’ that self-assemble are generally the same, so if the part is equivalent to an edge, then all the edges have the same size (length). We also suppose that in some situations it might be easier to assemble parts that result in planar surfaces than parts that have to contend with twisted surfaces that are out of plane or far out of plane. We used that logic to understand why the protein clathrin self-assembles into only certain fullerene cage structures and why the carbon atom self-assembles into only those cages that all have isolated pentagons. We are also interested in symmetry point groups that characterize cylinders, like nanotubes, as well as the icosahedral, octahedral and tetrahedral ones.
I have noticed that you have excluded most prisms and anti-prisms from your area of focus, it seems because of their lack of polyhedral symmetry. Is there anything about polyhedral symmetry specifically that you find to be important or interesting?
Good point. The Archimedean solids, like the soccer ball or truncated icosahedron, have one type of vertex and more than one type of regular face. Prisms and antiprisms do as well, but they do not have polyhedral symmetry. Polyhedral symmetry is appealing for reasons related to the prior answer. And, as Crick and Watson observed in 1956, virus shells (capsids) are likely to have helical or icosahedral symmetry because these elegant structures can be assembled from a very small number of parts, perhaps one in many cases, with a minimum of rules or genes.
A lot of media coverage of your findings have emphasized “400 years”. Where would you personally place the importance of the findings within the context of other polyhedron-related discoveries in the past 400 years? (For example,could you compare the new polyhedra with the Catalan Solids, Kepler’s Star polyhedra, Norman Johnson’s solids, Coxeter’s many findings, results in higher dimensional polytopes, etc).
All of these polyhedra are wonderful. Why compare?
There seem to be many potentially beneficial applications of your findings. Does this drive your research, the hope that the applications of your discovery can help humanity, or are you content with pure abstract discovery just for the sake of understanding geometry better and finding something new, regardless of how it changes the practical world?
We never gave any thought to applications. We are basic scientists interested in beautiful objects. However, now that we have something new, it makes sense to think about uses. For example, in our paper we cite a wonderful article in the NY Times that described spherical computer displays and associated software that help children and adults alike to understand changes in the earth and its climate. Think what would happen to the so-called “debate” about climate change if everyone (including our political leaders) could see it for themselves on the spherical display. These displays could be much less expensive and thus more widely used if they were made from chips (like the planar faces of the Goldberg polyhedra). Also, we wonder if the Goldberg polyhedra could be used as designs for inexpensive but beautiful housing in disaster areas.
Any indication yet that you are aware of that your findings could influence string theory, particle physics or cosmology?
No.
Concerning future research, do you anticipate that your method of transforming cages into polyhedra by adjusting dihedral angle discrepancies to zero, or similar methods, will lead to new findings in other aspects of geometry, such as new 2-dimensional tilings, or previously unknown higher dimensional polytopes? Is this an area of interest for you? Are there any other particular classes of polyhedra you are excited to explore?
It would be wonderful to extend the work to higher dimensions, but it is hard enough to think clearly about those objects without having to worry about metrical properties like edge length, angles in faces and planarity
Thank you, Stan. I will be looking forward to any new discoveries to which this may lead.
So, there you have it, folks. I guess the moral of the story is that if you sort through all of the noise and cynical trash out there, and if you are willing to put in a little extra effort and patience, pretty much anything you ever wanted to know is at your fingertips with the click of a button. And there are still plenty of new things to be discovered. Yes, journalism has become increasingly unreliable, but at the same time our ablity to simply do it ourselves is become increasingly easier. What a frustrating yet particularly wonderful and splendid time period to be alive!
I will now leave you with this quote from the great Johannes Kepler:
“We do not ask for what useful purpose the birds do sing, for song is their pleasure since they were created for singing. Similarly, we ought not to ask why the human mind troubles to fathom the secrets of the heavens. The diversity of the phenomena of nature is so great and the treasures hidden in the heavens so rich precisely in order that the human mind shall never be lacking in fresh nourishment.”
References:
Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses
(the original paper by Stan Schein and James Maurice Gayed)
http://www.pnas.org/content/early/2014/02/04/1310939111.abstract?sid=ecc1b2dc-28a3-4ffd-a274-31537de9daf3
Science News -Goldberg Variations
https://www.sciencenews.org/article/goldberg-variations-new-shapes-molecular-cages)
Scientific American article with video by George Hart about Goldberg Polyhedra (2013)
http://www.scientificamerican.com/article/goldberg-polyhedra-mathematical-impressions-video/
Gizmodo’s atrocious article
http://gizmodo.com/these-brand-new-shapes-are-a-class-of-their-own-1523136222








“How is it that this is what passes for journalism today? This guy just copied an article from another website, an article that was almost as far off from the truth, went further and misunderstood every detail of the first article, took no effort to check his facts, obviously did not consider looking at the original research paper, and turned in and published pure garbage. What is even the point of writing about something if literally every single sentence is wrong? Why is this considered acceptable? Why do we not have higher standards than this?”
Because it’s math. Most people don’t know how to write about math, and they assume that people will take in the gist and ignore everything else. A guy can paste and copy an incorrectly-written article, and it can pass through editors, because what are the odds that a copy-editor will have the knowledge needed to fact-check his article? The few that are paying attention may complain, but it will be few and far between, and if you get a response back, it’ll be a shrug and a half-assed “sorry”, or possibly a correction in the next edition that no one will notice. They assume no one cares, which is rather sad. The tweet about “piddling around” is particularly irritating. The “piddling around” that these men have been doing adds to the store of knowledge that man has created in order to understand the universe. What has that tweeter done lately to contribute to that store? Probably nothing.
“All of these polyhedra are wonderful. Why compare?” That’s a rather lovely ideology. I feel like the world would be a better place if more people adopted it as such.
“The tweet about ‘piddling around’ is particularly irritating.” Amen, sister! Especially coming from the asshole who spends his time on TWITTER…. God!!!
.
ADAM LORE! Great write-up, mate. As you might imagine, I find this both super-awesome and hard to understand. Some of the polyhedra in the illustrations are simply beautiful. I wonder if Jesus invented them…?
Thanks Jeff!
Some excellent points, Sarah. Thank you. They assume no one cares, which is largely true. The few who are paying attention notice, and nothing changes. A very sad state of affairs indeed.
“How is it that this is what passes for journalism today?”
It isn’t. I would think most people who know what journalism is would know that most of the bloggish trash that appears on Gizmodo and other Gawker sites isn’t it. Or at least I would hope so.
“Why do we not have higher standards than this?”
The downside to the streamlining and democratization of media brought to us by the Internet is that there are few barriers for bad information, and little profit to be made from good information. Ad revenue has abandoned news media, and so the mantra now is if you can do it cheaper and faster, you are doing it better. That means as little work, as little editing and, in the case of something like the Huffington Post, paying as few people as possible.
Or, to put it another way, do you pay to receive your news, or do you just get it for free? If it’s the latter, that might say something about your standards for journalism. Not to be snarky and not to pretend I don’t have a bias, but it is true what they say: you get what you pay for.
And as for Schein wondering about the interest about the story — (relatively) easy-to-understand science stories are red meat for most news outlets. They’re largely positive, they can run at any time and they have at least some interest to every reader out there. Consider when Pluto was downgraded from a planet — it meant almost nothing and it had no effect on anyone here on Earth, and yet it was a huge story. Why? It meant a little something to everyone. You tell someone a new shape has been found, and it’s sort of the same.
“It isn’t. I would think most people who know what journalism is would know that most of the bloggish trash that appears on Gizmodo and other Gawker sites isn’t it. Or at least I would hope so.”
Right, I agree, it isn’t journalism, but what I mean is that it is what is currently passing as journalism, it is largely accepted as being an acceptable replacement for good journalism. It is what shows up on Google News while quality articles do not.
I agree about the streamlining and democratization of the media, and the problems inherent in having it being free, I just wish more people would examine it and stop enabling the decreasing quality of everything.
This was a really interesting article. Thank you for removing the noise from all of the media chatter.
Thank you! I’m glad you found it to be interesting. :-)
Hey Adam! Long time no chat. It makes me happy to see a guest post of yours on here, especially one as interesting and well-written as this. I never would have guessed you had an interest in geometry.
Hey, thanks. Sorry, didn’t recognize your username, though. Do I know you from Youtube? Glad you enjoyed the article.
It (the decline of journalism in our time) is a double edged sword. As sources diversified, and audiences began to shrink, the quality of the articles/writing began to decline, as less time and money could be dedicated to/made from it. And so, as the quality in “traditional” journalism declined, so did the audience. I, for one, haven’t bought a newspaper – or paid a single cent for “news” – in at least three years. Prior to that, even, I was very sporadic in paying for my news, because I could see no point in it, thanks to the declining quality. So less income came to the news media organisations and so they were able to pay for less journalism… Sigh.
–
I studied to try to become a journalist, for a time, and I enjoy the actual DOING of the work, but the hard edged world and diminishing returns have made all the journalists (the ones I met anyway) into cynical, bitter, distasteful people and I vowed to never EVER enter that industry.
–
And I find it a little sad that the group of people feeding the minds of our society are in pursuit of the cheapest, most cynical, most sordid stories, purely to make money.
–
Love the article. I’ll have to read it again, methinks, to grasp it all, but I’m even looking forward to that.
Likewise wanted Connor McCulloch (Saint. Stephen Saint. Agnes, The state of virginia.), your coachable along with heady gambler from the MadLax club. In the event you knew just about anything about Huge, you’d learn it’s an far configurable resource and can also generate almost any good you’d like. Your current perhaps a BMTH fanboy exactly who required fatality aluminum also reared it is unpleasant mind fever currently brewing, “BRIE, BRIE, BRIEEEEE” doesn’t necessarily help make tunes this makes extravagant fontina. One doesn’t including dubstep? Which is nice.
What did you spam, oakley holbrook sunglasses for sale? Nice cheese sir. What did you spam? For cooking or in meals? Sprinkle it about.
Rachael Ray
Every day
Brilliant. But now I have to leave the spam, you bastard.
Really? You can’t delete it? Rachel Ray has stopped by more than once. Deletion and then execution is in order. Let me know if you need help with the latter.
Only a qualified celebrity chef should help with the execution of a spam platter.
This strongly supports the theory that latency is an advanced bet-hedging approach progressed by the virus over countless
years.